안녕하세요. 이번 포스팅에서는 저번 포스팅이 어려웠기 때문에, 복습하는 의미로 예제를 하나 들고왔습니다.

어느 한 미용실이 있다고 합시다.
미용실에는 커트를 진행하는 1 자리가 있고, 뒤에 기다릴 수 있는 자리가 4자리가 있습니다.
커트는 한 번에 항상 15분이 걸린다고 가정을 하고, 만약에 커트가 끝나고 기다리는 사람이 없다면, 미용사는 무조건 15분을 쉬고 일을 시작합니다.
그리고 15분 동안 손님이 올 확률은 다음과 같습니다.

그리고 State를 미용실에 있는 고객의 수라고 정의하면, 우리는 변환행렬을 정의할 수 있습니다.
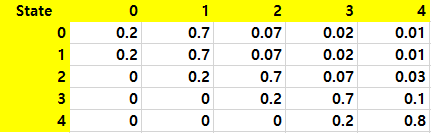
시간이 무한대로 지났을 때, 각 State로 배정될 확률을 steady state probability라고 정의합니다.
우리는 이를 행렬을 계속 곱하면서 얻을 수 있습니다.

이처럼 특정 값에 수렴함을 알 수 있습니다.
즉, 무한대의 시간이 지났을 때, 미용실에 0명이 있을 확률은 0.0899, 1명이 있을 확률은 0.3596, 2명이 있을 확률은 0.2247, 3명이 있을 확률은 0.1797, 4명이 있을 확률은 0.1460이 됩니다.
따라서 평균적으로 미용실에 있는 사람의 수는 다음과 같습니다.

하지만, steady state probability를 구할 때, 항상 행렬을 계속 곱해서 구하기에는 무리가 있겠죠?
행렬이 수렴한다는 사실을 이용해 steady state probability를 쉽게 구할 수 있습니다.


즉 A행렬의 역행렬을 곱하고 b를 곱해주면 steady state probability가 나옵니다.
'통계 이모저모 > 응용통계학' 카테고리의 다른 글
| [응용통계] 11. 마코프 체인 (Markov Chains) (5) (0) | 2019.06.15 |
|---|---|
| [응용통계] 10. 마코프 체인 (Markov Chains) (4) 연습문제 (0) | 2019.06.15 |
| [응용통계] 8. 마코프 체인 (Markov Chains) (2) (0) | 2019.06.14 |
| [응용통계] 7. 마코프 체인 (Markov Chains) (1) (0) | 2019.06.14 |
| [응용통계] 6. 지수분포 (Exponential Distribution) (2) (0) | 2019.05.28 |



