728x90
1. Principal Component Analysis (PCA)
# PCA
# age credit_amount duration_in_month installment_rate num_of_existing_credits num_of_people_liable present_residence
german <- read.csv('German_credit.csv')
german_1 <- german[, c(3,6,9,12,14,17,19)]
summary(german_1)
Duration_in_month Credit_amount Installment_rate Present_residence Age
Min. : 4.0 Min. : 250 Min. :1.000 Min. :1.000 Min. :19.00
1st Qu.:12.0 1st Qu.: 1366 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:27.00
Median :18.0 Median : 2320 Median :3.000 Median :3.000 Median :33.00
Mean :20.9 Mean : 3271 Mean :2.973 Mean :2.845 Mean :35.55
3rd Qu.:24.0 3rd Qu.: 3972 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:42.00
Max. :72.0 Max. :18424 Max. :4.000 Max. :4.000 Max. :75.00
Num_of_existing_credits Num_of_people_liable
Min. :1.000 Min. :1.000
1st Qu.:1.000 1st Qu.:1.000
Median :1.000 Median :1.000
Mean :1.407 Mean :1.155
3rd Qu.:2.000 3rd Qu.:1.000
Max. :4.000 Max. :2.000
german_scaled <- scale(german_1, center = TRUE, scale = TRUE)
plot(german_scaled)
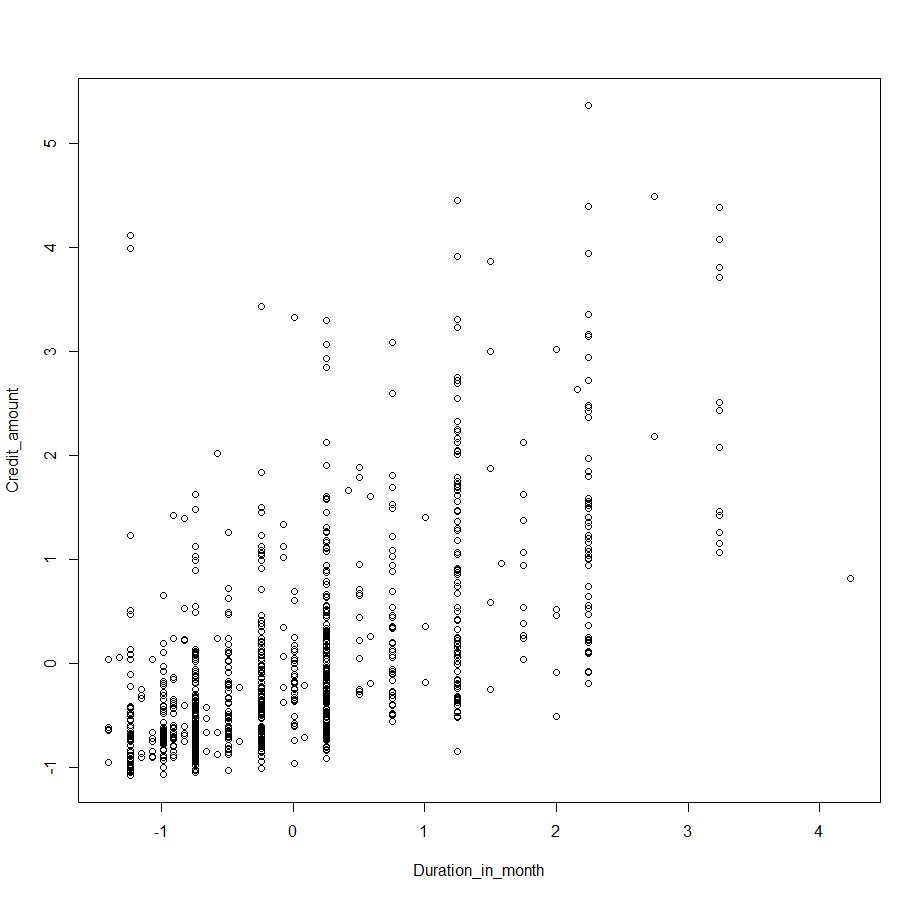
scale 함수를 통해서, 데이터를 정규화 시킬 수 있습니다.
dat_cov = cov(german_scaled)
dat_cor = cor(german_scaled)
PCA는 데이터의 공분산 행렬이나, 상관계수 행렬을 필요로 합니다.
pca_cov <- prcomp(german_scaled, covmat=dat_cov) # cov # stdev2 = lambda
pca_cor <- prcomp(german_scaled, covmat=dat_cor) # corr # stdev2 = lambda
PCA는 R에서 prcomp 함수를 통해서 모델링 가능합니다.
eigenv <- pca_cor$sdev^2
x <- seq(1:ncol(german_scaled)) # x축
plot(x, eigenv, main="Scree plot", type="b", xlab="Number", ylab="Eigen value")
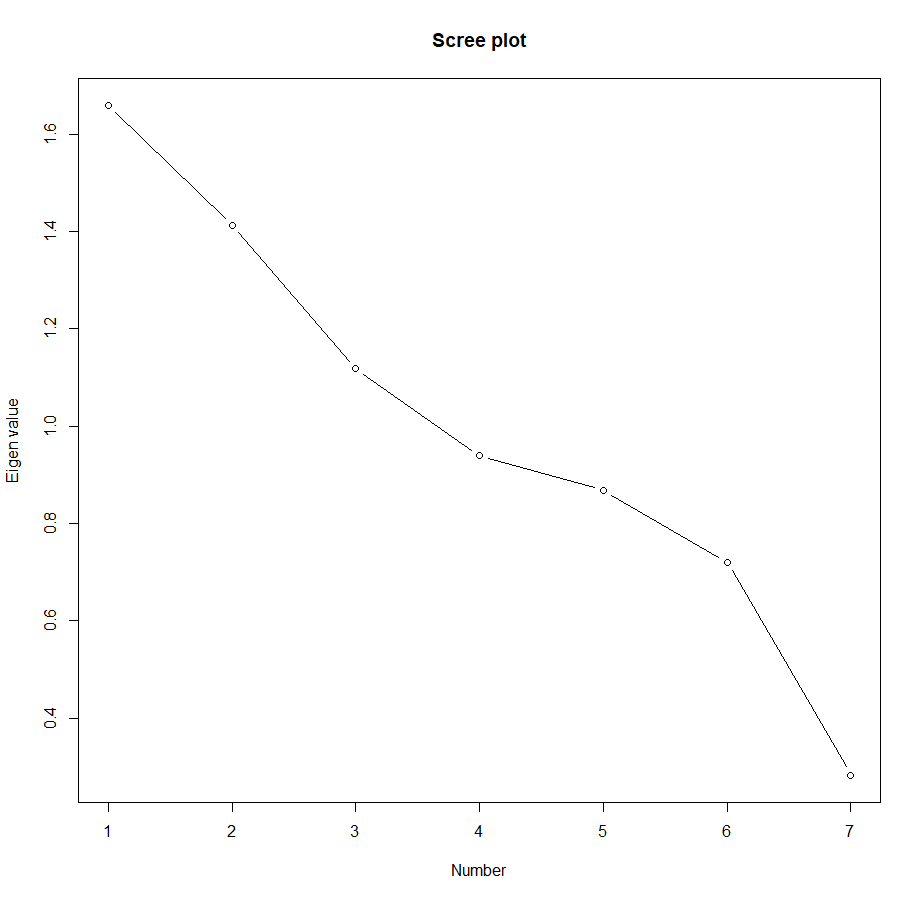
PC 들의 표준편차를 불러와서, 제곱해주면 Eigenvalue 를 구할 수 있고, 선택되는 PC의 순번에 따라 Eigenvalue의 변화를 관찰합니다.
plot(pca_cor, type="lines")
위의 코드로 한 번에 위의 plot을 그릴 수도 있습니다.
biplot(pca_cor)
biplot 함수는 PC1과 PC2에 대한 Score plot을 그려줍니다.
summary(pca_cor)
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.288 1.1885 1.0574 0.9691 0.9318 0.8489 0.53148
Proportion of Variance 0.237 0.2018 0.1597 0.1342 0.1240 0.1029 0.04035
Cumulative Proportion 0.237 0.4388 0.5985 0.7327 0.8567 0.9597 1.00000summary 함수는 PC들의 분산에 대한 누적 비율을 한 눈에 보여줍니다.
2. Factor Analysis
fa_g <- factanal(german_scaled, factors=3, rotation="varimax", scores = "regression") # varimax is the default
Factor analysis 는 factanal 함수를 사용하여, 모델링 할 수 있습니다.
load <- fa_g$loadings
load
Loadings:
Factor1 Factor2 Factor3
Duration_in_month 0.985 0.152
Credit_amount 0.672 -0.223
Installment_rate 0.994
Present_residence 0.379
Age 0.685
Num_of_existing_credits 0.235
Num_of_people_liable 0.182
Factor1 Factor2 Factor3
SS loadings 1.430 1.071 0.708
Proportion Var 0.204 0.153 0.101
Cumulative Var 0.204 0.357 0.458결과를 loading attribute에서 뽑아낼 수 있습니다.
plot(load[,1:2],type="n") # plot factor 1 by 2
text(load[,1:2],labels=colnames(german_scaled),cex=.7) # add variable names
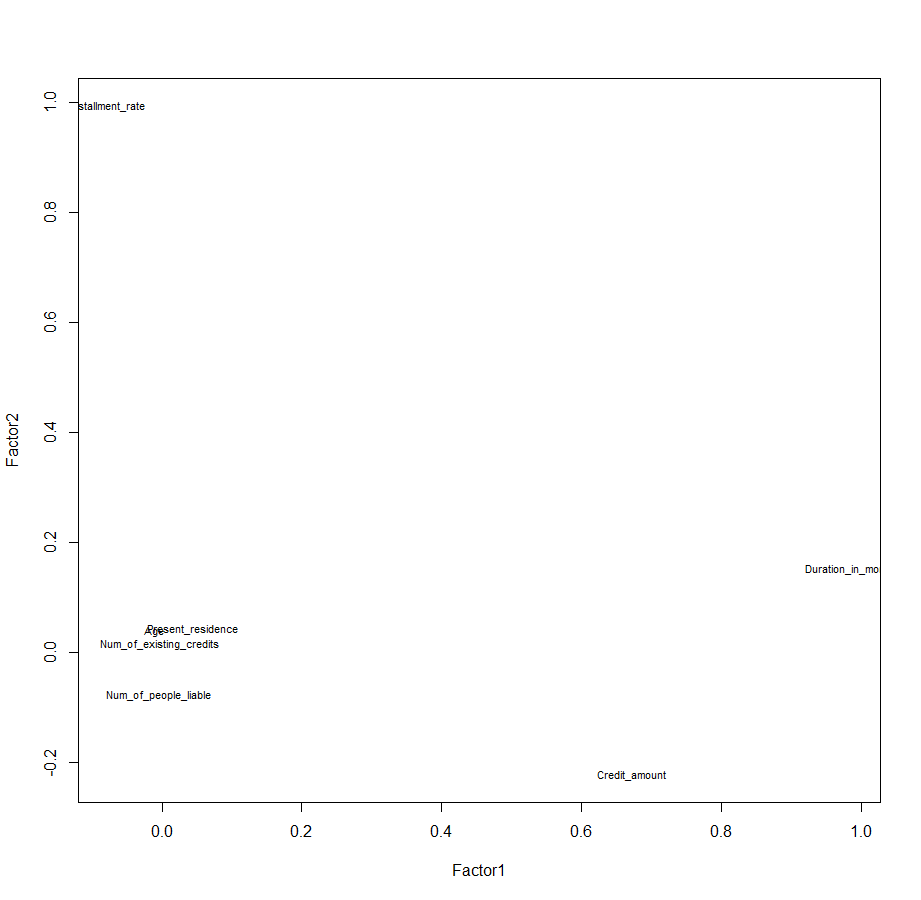
각 변수들을 factor 1 과 factor 2에 대해 표현할 수 있습니다.
Duration_in_month 와 Credit_amount는 Factor 1과 큰 관련이 있네요.
'데이터 다루기 > Base of R' 카테고리의 다른 글
| [R] K-nearest neighbor (KNN) method (0) | 2020.04.07 |
|---|---|
| [R] Hierarchical clustering, K-means clustering (0) | 2020.03.16 |
| [R] Ridge, Lasso, ElasticNet Regression (1) | 2020.03.09 |
| [R] Data Partition (데이터 분할) (0) | 2020.03.09 |
| [R] 회귀 분석 (변수선택) (0) | 2020.03.08 |

