본 포스팅은 STATQUEST 유튜브 채널을 참고하였습니다.

위의 데이터에 대해서 3가지 input attribute로 Love troll 2를 예측하고자 한다.
Classification Task 이므로 오차 함수를 Cross Entropy로 정의한다.

Step 1)
▶ 모델에 대한 초기 예측 값을 정해야 하는데, 오차를 최소화하는 값으로 정하자.
▶ Classification Task에서는 Logistic Regression과 마찬가지로, log(odds)를 사용한다.


▶ 따라서, 위의 케이스에서 초기 예측 값은 다음과 같다.

Step 2)
A)
▶초기 오차를 구하면 y_i - p 와 같다. 위 경우에서 p = 0.67 이므로 Residual은 다음과 같다.

B)
▶ Regression Tree를 적합 해서, 오차 값들을 각 Region으로 분할
▶ 위 경우 관측치가 적어서 2개의 leaf를 사용했지만, 보통 8 ~ 32개의 leaf를 사용함

C)
▶ 각 Region별로 어떤 예측 값이 출력 되야 할까?

▶ 위 식을 gamma로 미분하는 것은 어려움이 있으므로, Second order Taylor Polynomial을 사용.

▶ 위에서 분자는 Residual 값임을 증명하였다. 분모의 값만 계산해보도록 하자.

▶ 따라서 감마의 값은 다음과 같이 주어진다.
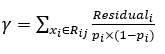
▶ 이제 위의 케이스에서 각 Region의 값을 구해보자.

D)
▶ 이제 예측 값이 업데이트가 되는데, Overfitting을 막기 위해 Learning rate가 가중된다.

▶ 예를 들어서, R(1,1)에 속한 관측치는 0.69 + 0.8 X 1.5 = 1.89 로 업데이트가 된다.
▶ 참고로, 이를 확률 값으로 바꾸면, p = 0.87 이 된다.
'데이터 다루기 > 머신러닝 이론' 카테고리의 다른 글
| [Machine Learning] XGBoost (2) Methematical details (0) | 2020.10.05 |
|---|---|
| [Machine Learning] XGBoost (1) Algorithm Schema (0) | 2020.10.05 |
| [Machine Learning] Gradient Boosting (Regression) (0) | 2020.09.27 |
| [Machine Learning] AdaBoost (0) | 2020.09.27 |
| [Machine Learning] Boosting (부스팅) (0) | 2020.09.21 |



