본 포스팅은 STATQUEST 유튜브 채널을 Reference하여 만들었습니다.

XGBoost는 Gradient Boosting 알고리즘을 기반으로 하고 있음.
일반적인 Gradient Boosting과의 차이점은 Training algorithm 개선되었고, Optimization Technique이 추가되었음.
A. Regression Task.

Drug Dosage로 Drug Effectiveness를 예측하는 Task를 가지고, 4개의 관측치가 있다.
XGBoost는 초기 예측을 Regression, Classification 모두 default로 0.5의 값으로 설정함.
이제 오차를 계산하고, 하나의 Leaf에 전부 집어넣는다.

a) XGBoost Tree
XGBoost는 Regression Tree를 새롭게 구성하는데, XGBoost Tree라고 정의한다.
Gradient boosting에서 Regression Tree는 Gini index로 Tree를 구성했다.
XGBoost Tree는 Similarity Score라는 Index로 Tree를 구성한다.

Lambda는 Regularization Parameter로 overfitting을 방지하는 역할을 한다. (이후 자세히)
Similarity Score의 유도 과정은 이후에 보이도록 하겠다.
우선 위의 케이스에 대해서 Tree를 구성해보자. (Lambda는 편의상 0의 값을 주겠음.)


이제 Tree를 확장시키는 규칙을 정해보자.
모든 규칙에 대해서 Gain 값을 계산한 후, 가장 높은 Gain 값을 가진 규칙이 선택된다.


위의 경우에서는 Gain이 가장 큰 (1) 규칙으로 확장된다.
같은 방식으로, Gain이 음수가 되지 않을 때까지 Tree를 확장하면 다음과 같다.

이렇게 Tree를 최대한 확장하였으면, 이제 Prune을 해야 한다.
Regularization parameter Gamma 에 대해 Gain-Gamma < 0 인 경우 규칙을 Prune 한다.

즉 위 경우에서 Gamma를 130으로 정의하면, 첫 번째 규칙의 Gain이 120.33 이지만 두 번째 규칙의 Gain이 140.17이기 때문에 Prune은 발생하지 않는다.
반면에 Gamma를 150으로 정의하면 모든 규칙이 Prune되고, 4개의 오차는 하나의 예측 값으로 예측된다.
☎ 여기서 가 0이 아니라면 어떻게 될까? (Lambda = 1)
우선 첫 Leaf에서의 Similar score가 달라진다.

그리고 Gain을 다시 계산함으로써, 어떤 규칙으로 확장되는가를 정해보자.
이 때, 1개의 observation만 포함되던 Leaf의 분모는 (1+1)이 되므로, Similarity score가 절반으로 줄어든다.
즉, 다시 말해 는 적은 observation을 가지는 노드를 덜 만들어지게 하는 역할을 한다.
위의 Case에서는 Similarity score가 많이 감소하였지만, 여전히 1번 규칙이 선택된다.

b) Tree Update
다시 위의 XGBoost Tree로 돌아가서, 최종적으로 Leaf의 Observation이 어떠한 값으로 Update 되는지를 알아보자.
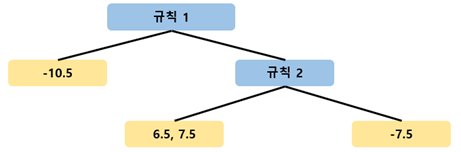

Lambda = 0의 경우, 기존 Gradient Boosting과 마찬가지로 평균 값을 반환한다.

예측 값에 Learning rate를 곱해준 후, 초기 예측 값에 더해주어, Update한다.

B. Classification Task.

Drug Dosage로 Drug Effectiveness를 예측하는 Task를 가지고, 4개의 관측치가 있다.
XGBoost는 초기 예측을 Regression, Classification 모두 default로 0.5의 값으로 설정함.
이제 오차를 계산하고, 하나의 Leaf에 전부 집어넣는다.

a) XGBoost Tree

Regression Task에서와 마찬가지로, 계산의 편의상 Lambda = 0 을 설정하도록 한다.
초기 Leaf의 Similarity score를 구해보자. 이 때, 분자가 0이므로 0의값을 가진다.

Gain을 최대화하는 방향으로 Tree를 확장해보자.

Gamma 를 2로 정의하면 두 규칙 모두 살아남는다.
a) Tree Update
Tree가 완성되었으므로, 각 Leaf 별로 Output을 계산해보자.

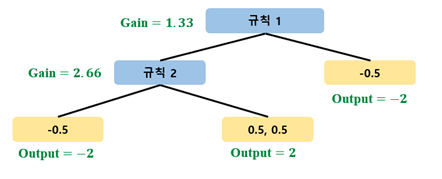
이제 예측 값의 Update는 Gradient Boosting for classification과 마찬가지로 log(odds) 사용.
우선 초기 예측 0.5의 log(odds)를 계산하면

예측 값에 Learning rate를 곱해준 후, 초기 예측 값에 더해주어, Update한다.
예를 들어, 규칙 2의 왼쪽 관측치는 Learning rate가 0.8일 경우 다음과 같은 업데이트가 발생한다.

'데이터 다루기 > 머신러닝 이론' 카테고리의 다른 글
| [Machine Learning] XGBoost (3) Optimization technique (0) | 2020.10.05 |
|---|---|
| [Machine Learning] XGBoost (2) Methematical details (0) | 2020.10.05 |
| [Machine Learning] Gradient Boosting (Classification) (0) | 2020.09.27 |
| [Machine Learning] Gradient Boosting (Regression) (0) | 2020.09.27 |
| [Machine Learning] AdaBoost (0) | 2020.09.27 |



