이번 포스팅은 이전 포스팅에서 공부했던, Similarity Score와 Output value의 식을 유도하겠다.
Gradient boosting에서 Output value를 찾기 위해 다음 식을 최소화하는 Gamma를 미분으로 찾았다.

XGBoost는 Regularization term이 추가되어, 식이 약간 변형된다.
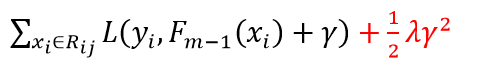
Gradient boosting에서는 위를 Optimization 하기 위해서 에 대해서 미분을 하였다.
이 때, Classification에 대해서만, Second order Taylor Polynomial을 활용하였다.
하지만 XGBoost는 Regression 또한 Second order Taylor Polynomial를 활용한다.

표기의 용의성을 위해 다음과 같이 정의해보자.

Regression task의 경우, 손실 함수는 MSE로 정의된다.


Classification task의 경우, 손실 함수는 Cross Entropy로 정의된다.


이제 Similarity score를 유도해보자.
우리는 지금까지의 과정에서 Loss function을 최소화하는 Output (Gamma) 를 찾았다.
Similarity score는 그 이후 단계로, Loss function의 위치를 최소화하는 것에 의미를 둔다.
이 때, -1을 곱해줌으로써, 최대화하는 방향으로 식을 변형시킨다.

상수항은 식에 영향을 주지 못하므로 제거하고 Gamma에 위에서 구한 값을 대입하자.
위 식을 풀면 Similarity Score를 얻을 수 있다.

'데이터 다루기 > 머신러닝 이론' 카테고리의 다른 글
| 하이퍼 파라미터 튜닝 (1) (0) | 2021.11.22 |
|---|---|
| [Machine Learning] XGBoost (3) Optimization technique (0) | 2020.10.05 |
| [Machine Learning] XGBoost (1) Algorithm Schema (0) | 2020.10.05 |
| [Machine Learning] Gradient Boosting (Classification) (0) | 2020.09.27 |
| [Machine Learning] Gradient Boosting (Regression) (0) | 2020.09.27 |



