728x90
반응형
Generalizd method of moments (GMM)을 배우기 앞서, 식 하나로 요약해서 정리하면 아래와 같다.

이 때, 함수 f는 moment condition을 나타낸다.
그렇다면 우선, moment condition에 대해서 정의를 해야한다.
우리는 적률이 무엇인지를 안다는 전제하에 진행하도록 하겠다.
moment condition이란 관측치 Y와 모수 theta에 대한 함수로써, 기댓값을 취하였을 때, 0을 가지는 조건을 만족한다.

GMM의 기본적인 아이디어로, E를 표본평균으로 대체한다.

대수의 법칙에 의해서 Sample size: T가 무한대로 커짐에 따라, 위 두식은 같아진다.
위 조건을 최대한 만족하기 위해서, moment condition을 최대한 0에 가깝에 만들어주는 모수 theta를 추정하는 것이 GMM이다.
이를 위해, m(theta)를 제곱하여 최소화 하는 theta를 찾자.

이 때, W는 positive-definite weighting matrix로, moment를 가중합 시키는 행렬이다.
일반적으로 Identity matrix를 주로 사용한다.
위식을 정리하면, 맨 처음 보여준 식으로 정의된다.
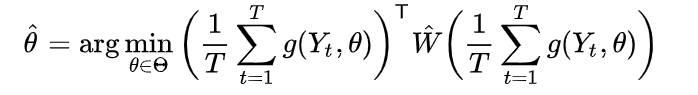
반응형
'통계 이모저모 > 공간 통계' 카테고리의 다른 글
| [공간 통계] 11. Spatial Autoregressive model with GMM (0) | 2020.03.05 |
|---|---|
| [공간 통계] 9. Spatial Autoregressive model (0) | 2020.02.19 |
| [공간 통계] 8. 공간 회귀 분석 (Spatial regression) (0) | 2020.02.18 |
| [공간 통계] 7. Heterogeneity (0) | 2020.02.18 |
| [공간 통계] 6. Getis-ord (0) | 2019.09.09 |


