728x90
반응형
[Ref] 수리통계학 (송명주, 전명식)
안녕하세요, 이번 포스팅은 지난 포스팅에 이어서 연속형 확률분포를 다룰 계획입니다.
이번 확률분포는 지수분포 (Exponential distribution) 입니다.
지수분포는 앞서 배운 포아송 분포와 아주 밀접한 관련이 있습니다.
포아송 분포가 어떤 분포였는지 기억나시나요??
2019/05/23 - [통계 이모저모/수리통계학] - [수리통계학] 10. 이산형 확률분포 (2) 포아송 분포
그렇습니다! 포아송 분포는 특정 시간동안 발생할 사건의 수에 대한 분포였다면, 지수분포는 특정 사건이 발생하는데 걸리는 시간에 대한 분포입니다.

이 때, λ 는 포아송 분포에서의 모수와 같다고 생각하시면 됩니다. 즉, 특정 시간동안 발생하는 사건의 수입니다.
지수분포는 Θ=1/λ 로 치환하여 표현되기도 합니다.
이제 지수분포의 기댓값과 분산을 구해보도록 하겠습니다.
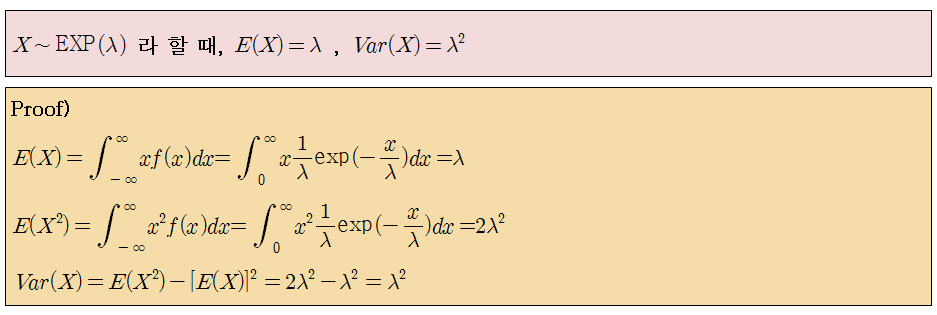
마지막으로, 지수분포는 기하분포와 같은 성질을 가지고 있습니다.
기하분포의 성질 기억나시나요??
바로 비기억성입니다.
예를 들어서, 버스가 도착 시간의 간격이 지수분포 30분을 따른다고 할 때, 20분동안 기다린 후에도 여전히 기다리기 전과의 버스 올 때까지의 걸리는 시간에 대한 분포는 같다는 것입니다. (신기하죠??)

반응형
'통계 이모저모 > 수리통계학' 카테고리의 다른 글
| [수리통계학] 16. 연속형 확률분포 (4) 감마분포, 베타분포 (1) | 2019.05.26 |
|---|---|
| [수리통계학] 15. 연속형 확률분포 (3) 정규분포 (0) | 2019.05.24 |
| [수리통계학] 13. 연속형 확률분포 (1) 균일분포 (0) | 2019.05.24 |
| [수리통계학] 12. 이산형 확률분포 (4) 초기하분포 (0) | 2019.05.24 |
| [수리통계학] 11. 이산형 확률분포 (3) 기하 분포, 음이항 분포 (0) | 2019.05.24 |



