[수리통계학] 19. 적률

[Ref] 수리통계학 (송명주, 전명식)

안녕하세요, 이번 포스팅은 적률생성함수을 배워보기에 앞서 적률에 대한 개념을 짚어보는 시간을 가져보도록 하겠습니다.

적률생성함수는 수리통계학 뿐만 아니라 통계에서 굉장히 중요한 개념이므로 정확히 알아야 합니다.

적률의 정의는 위와 같습니다. 정의만 보면 이게 무엇을 의미하는지 모를 수 있습니다.

한마디로 정의하자면 적률은 분포의 특징을 설명해주는 지표입니다.

예를 들어서, 1차적률은 확률변수의 평균을 나타내며, 2차 중심적률은 분산, 3차 중심적률은 왜도(skewness), 4차 중심적률은 첨도(kurtosis)가 됩니다.

이 때 왜도는 확률밀도함수의 비대칭성을 나타내는 척도이며, 첨도는 뾰족한 정도를 재는 척도입니다.

https://ko.wikipedia.org/wiki/%EB%B9%84%EB%8C%80%EC%B9%AD%EB%8F%84

 

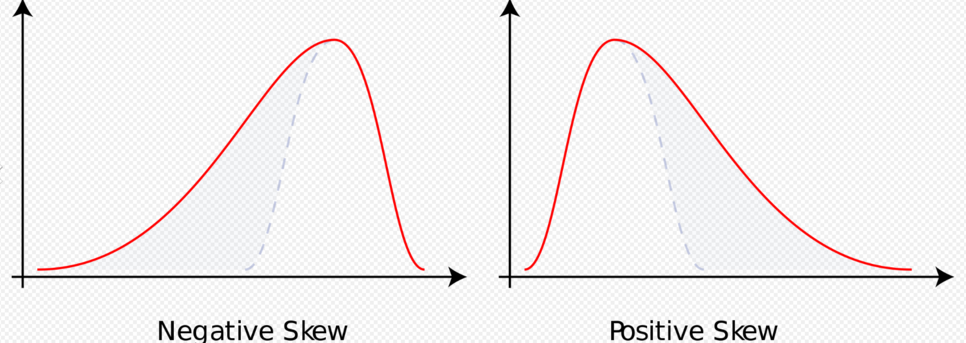
양의 왜도와 음의 왜도에 대한 해석은 위와 같습니다.

http://www.ktword.co.kr/abbr_view.php?m_temp1=4375

 

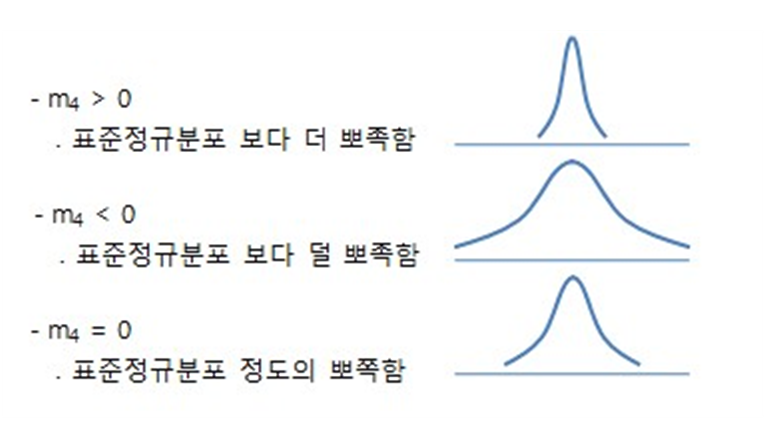
첨도 또한 위의 그림으로 해석됩니다.

​