[머신러닝] 선형 회귀 분석 (2)

안녕하세요, 선형 회귀 분석 두번째 시간입니다. 이번 시간에는 선형회귀분석의 적합과 성능 평가에 대해서 알아보도록 하겠습니다.

선형 회귀 분석은 실제값과 예측값 사이의 오차 제곱들의 합 (SSE)을 최소로 하는 β를 추정하게 됩니다.

이 포스팅에서는 머신러닝에서의 선형 회귀 분석의 활용을 다루기 때문에 자세한 수리적 내용을 생략하도록 하겠습니다.

이 과정의 자세한 내용은 통계의 회귀 분석 파트에서 다루도록 하겠습니다.

​

https://vitalflux.com/40-regression-analysis-interview-questions-for-data-scientists/

 

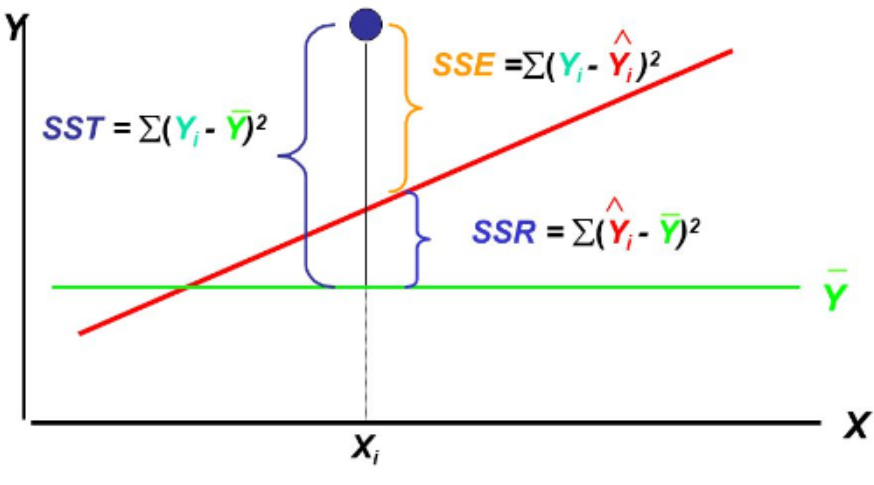
선형회귀분석의 성능을 측정하는 지수로 결정계수 (R2: R-squre)가 있습니다.

결정계수이 가지는 의미를 쉽게 설명하자면, 우리가 일반적으로 Y값을 예측한다고 할 때, Y의 평균으로 예측하는것이 일반적이잖아요?

결정계수는 우리가 선형회귀모형으로 예측한 값이 그냥 평균으로 예측한 값보다 얼마나 정확할까를 의미합니다.

SST는 실제값과 Y들의 평균값과의 차이, 즉 Y의 평균으로 예측했을 때 얼마나 정확할까를 나타냅니다.

SSE는 실제값과 선형회귀모형의 예측값과의 차이, 즉 선형회귀모형으로 예측했을 때 얼마나 정확할까를 나타냅니다.

SST와 SSE는 그 값이 작을수록, 각 예측의 정확도가 높다고 할 수 있습니다.

SSR은 선형회귀모형의 예측값과 Y들의 평균값과의 차이, 선형회귀모형으로 예측했을 때와, Y의 평균으로 예측했을 때의 차이를 나타냅니다.

$\combi{R}^2=1-\frac{SSE}{SST}$R2=1−SSESST​​

위의 결정계수 식을 보시면, 1-(선형회귀모형으로 예측했을 때 얼마나 정확할까)/(평균으로 예측했을 때 얼마나 정확할까)로 나타내는데, 선형회귀모형이 정확하다면, SSE가 작아지고, R2의 값은 커지는 것을 유추할 수 있습니다.

​

R2의 값은 보통 1보다 작거나 같은데, 1에 가까울수록 회귀모형의 성능이 좋다고 할 수 있습니다.

http://nutricionmascotas.com/science/what-is-delta-r-squared-in-regression.php

 

하지만 R2는 변수의 개수가 많아질수록 항상 높아진다는 단점이 있습니다.

이 때문에, overfitting문제가 발생합니다.

이 때문에, 제안된 것이 변수의 개수 p를 추가한 adjusted R-square입니다.

p가 커지면 빼는값의 분모가 작아지면서 빼는 값이 커지게되고 adjusted R-square이 감소합니다.

따라서, 변수의 개수를 패널티항으로 받아들입니다.

​

이 이외의 것으로, Mellows CP, AIC, BIC등도 있습니다.

​