안녕하세요, 이번 시간부터는 선형 회귀 분석에 대해서 알아보도록 하겠습니다.
일반적으로 회귀 분석은 독립 변수 x = (x1, x2, ···, xp)가 주어질 때, 종속 변수 y의 조건부 기댓값 (E(yⅠx))를 추정하는 것을 말합니다.
즉, 쉽게 말해서 데이터 x가 주어질 때, 가질 수 있는 y값의 기댓값을 추정한다는 것입니다.
따라서, 회귀 모형의 추정식은 다음과 같습니다.

회귀 모형을 추정할 때에, 데이터의 개수 n이 p보다 작은 경우, 굉장히 많은 solution이 존재하기 때문에, β가 불안정하게 됩니다.
n=p 인 경우, 만약 x들이 서로 선형 독립이라면, y = f(x,β)가 완벽하게 풀리게 되며 유일한 solution을 얻을 수 있습니다.
가장 흔한 경우인 n>p인 경우에는 정확한 solution이 존재하지 않기 때문에, β를 추정할 때 실제값과의 오차가 최소가 되도록 추정합니다.
마지막으로 선형 회귀 분석의 정의를 알아보도록 하겠습니다.
선형 회귀 분석의 정의에 대해서 잘못 알고 계신분들이 많은 것으로 알고 있기에 이번에 확실히 알도록 합시다!!
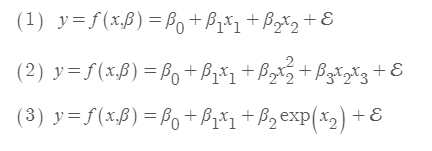
위의 3가지중에서 (1)이 선형인 것은 모두 알겠지만, (2),(3)이 선형인가? 라고 생각하는 사람도 많을것이다.
우선 정답을 알려드리면 선형이 맞다. 왜냐하면 선형의 기준은 β이기 때문에, β에 대해서는 (1),(2),(3) 모두 선형이기 때문이다.

즉 (4),(5) 의 경우에는, β에 대하여 선형이 아니기 때문에 비선형이라고 할 수 있다.
'데이터 다루기 > 머신러닝 이론' 카테고리의 다른 글
| [머신러닝] 능형 회귀 모형 (Ridge Regression) (0) | 2019.06.12 |
|---|---|
| [머신러닝] 선형 회귀 분석 (2) (0) | 2019.06.12 |
| 모델 평가 (1) | 2019.06.11 |
| Bias & Variance Trade-off (0) | 2019.06.11 |
| Reducible and Irreducible Errors (0) | 2019.06.10 |



