728x90
반응형
[Ref] 수리통계학 (송명주, 전명식)
이번 포스팅에서는 확률론과 통계학에서 매우 중요하다고 여겨지는 중심극한정리 (Central limit theorem)에 대해서 배워보도록 하겠습니다.

중심극한정리의 증명은 수리통계학의 수준을 벗어나므로 모르셔도 됩니다!
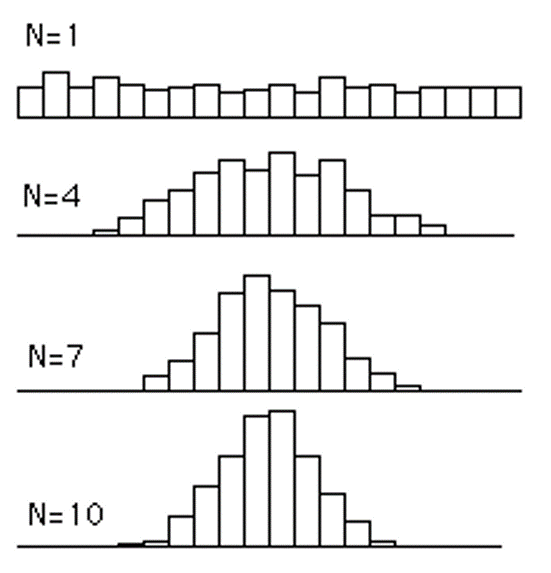
https://towardsdatascience.com/understanding-the-central-limit-theorem-642473c63ad8
중심극한정리는 평균과 분산이 주어진 모집단에서 표본의 크기가 매우커지면 그 평균과 분산을 가지는 정규분포로 수렴한다는 의미입니다.
예를 들어서 10000명의 몸무게에 대한 평균과 분산이 65kg, 10kg이라고 합시다.
그 때, 100개의 표본을 뽑아서, 그 들의 표본평균과 표본분산은 정확히 65kg, 10kg이 되지는 않습니다.
하지만 100개의 표본들이 매우 많아지면 표본들이 평균과 분산이 65kg, 10kg인 정규분포를 따른다는 것입니다.
반응형
'통계 이모저모 > 수리통계학' 카테고리의 다른 글
| [수리통계학] 26. F분포 (0) | 2019.05.27 |
|---|---|
| [수리통계학] 25. 카이제곱 분포 (0) | 2019.05.27 |
| [수리통계학] 23. 대수의 법칙 (0) | 2019.05.27 |
| [수리통계학] 22. 모집단과 표본 (0) | 2019.05.27 |
| [수리통계학] 21. 적률생성함수 (2) (2) | 2019.05.26 |



